https://www.acmicpc.net/problem/3020
3020번: 개똥벌레
개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종유석과 석순이
www.acmicpc.net

풀이 방식
나는 처음에는 1...n 구간마다 장애물로 막혀 있는 곳의 위치들을 높이별로 빈도수 배열을 구한 뒤 배열 전체를 검색하면서 최솟값과 그 개수를 구하는 방식으로 구현했었다.
// 완전 탐색으로 구현할 경우 O(n^2) 복잡도
for i in 0..<n {
var input = Int(readLine()!)!
if i%2 != 0 {
input = m - input
for j in input+1...m {
sumArr[j] += 1
}
} else {
for j in 1...input {
sumArr[j] += 1
}
}
}
var min = Int.max;
var count = 0;
for i in 1..<sumArr.count {
if sumArr[i] == min {
count += 1
continue
} else if sumArr[i] < min {
min = sumArr[i]
count = 1
}
}
print("\(min) \(count)")
하지만 이렇게 구현할 경우 모든 구간을 검색하면서 장애물의 길이만큼 작업을 해줘야 하기 때문에 시간복잡도 O(n^2)에 가까운 결과가 나온다.
이보다 좀 더 시간복잡도가 낮은 접근 방법으로는 누적합을 활용하는 방법이 있다. 누적합을 활용하기 위해서 먼저 천장에 붙어 있는 장애물만 먼저 살펴보자.
가장 긴 장애물, 즉 가장 아래까지 이어져 있는 장애물은 천장까지 이어지기 때문에 아래에서 위로 올라가면서 장애물의 합을 구할 때 누적이 된다. 그 말인 즉슨 아래에서부터 올라가면서 부딪히게 되는 벽들의 합은 곧 누적 합의 원리로 계산할 수 있다는 이야기.
마찬가지로 바닥에서 시작하는 장애물 또한 반대로만 생각하면 누적합의 원리로 계산할 수 있다.
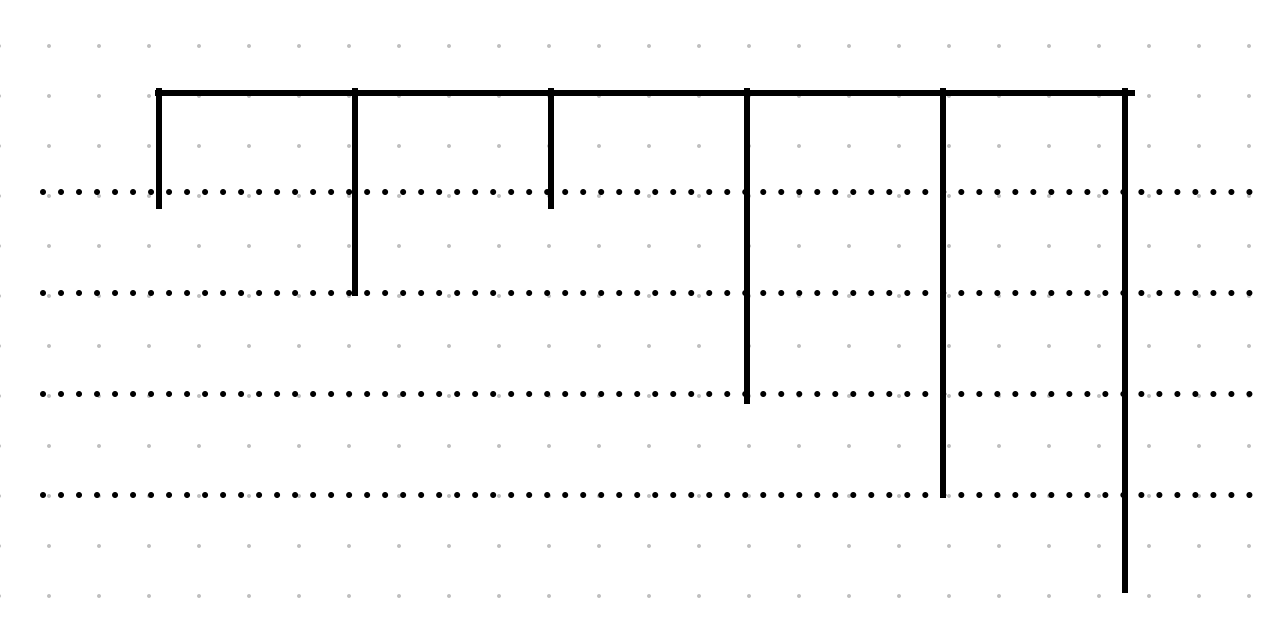
누적합의 시작점은 각각 천장에서 가장 멀리 떨어진 지점, 바닥에서 가장 멀리 떨어진 지점에서부터 시작하면 된다.
var bottomArr = [Int](repeating: 0, count: m+1)
var upArr = [Int](repeating: 0, count: m+1)
var lowerBound = m
var upperBound = 0
for i in 0..<n {
var input = Int(readLine()!)!
if i%2 != 0 {
input = m - input + 1
upArr[input] += 1
if lowerBound > input {
lowerBound = input
}
} else {
bottomArr[input] += 1
if upperBound < input {
upperBound = input
}
}
}
그리고 각각 누적합을 구한다.
var btmPsum = [Int](repeating: 0, count: m+1)
var topPsum = [Int](repeating: 0, count: m+2)
for i in lowerBound...m {
topPsum[i] = topPsum[i-1] + upArr[i]
}
for i in 0...upperBound {
btmPsum[upperBound-i] = btmPsum[upperBound-i+1] + bottomArr[upperBound-i]
}
마지막으로 높이별로 누적합을 통해 구한 천장 장애물 수와 바닫 장애물 수를 더하고 그 값을 기반으로 최솟값과 그 개수를 구한다.
var min = Int.max
var count = 1
for i in 1...m {
let obstacleCnt = btmPsum[i] + topPsum[i]
if( min == obstacleCnt) {
count += 1
} else if( min > obstacleCnt ) {
min = obstacleCnt
count = 1
} else {
}
}
print("\(min) \(count)")'Data Structure & Algorithm > 백준' 카테고리의 다른 글
| [Swift] 백준 16139 : 인간-컴퓨터 상호작용 (0) | 2023.12.18 |
|---|---|
| [Swift] 백준 10986 : 나머지 합 (0) | 2023.12.13 |
| [Swift] 백준 2559 : 수열 (2) | 2023.12.07 |
| No7662 이중 우선순위 큐 (0) | 2022.11.23 |
| No7576 토마토 (너비 우선 탐색) (0) | 2022.11.21 |


